#1. Interface(API / ADT) vs Data Structure
Interface
- Specification
- What data can store
- What operations are supported & what they mean
- Problems
DataStructure
- Representation
- How to store data
- Algorithms to support operations
- Solutions
#2. main interfaces
set
sequence
2 main DataStructures approaches
- arrays
- Pointer based
Static sequence interface
maintain a sequence of items X0, X1, X2 ... Xn-1 subject to these operations
- build(x): make new DS(DataStructure) for items in X
- len(): return n
- Iter_seq(): output X0, Xn ... Xn-1 in sequecne order(at least linear time)
- get_at(): return Xi (index i)
- set_at(): set Xi to X
- get_first/last()
- set_first/last(x)
Solution(natural): static array
- O(i) per get_at/set_at/len
- O(n) per build/iter_seq
Memory allocation model
allocate static array of size n in Θ(n) time
- space = O(time)
Key : word RAM model of computation
memory = array of w-bit words
"array" = Consecutive chunk of memory
array[i] = memory[address(array) + i]
array access is O(i) time
Assume w >= log n
Dynamic sequnce interface
Static sequence interface(upper that mentioned), plus
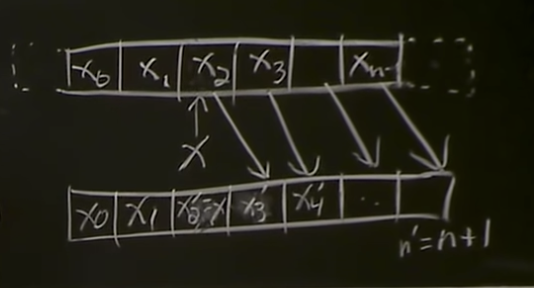
- insert_at(i, x): make x the new xi, shifting Xi -> Xi+1 -> Xi_2 ... -> Xn-1 -> Xn`-1
- delete_at(i): shift Xi <- Xi+1 <- ... <- Xn`-1 <- Xn-1
- Insert/delete_first/last(x)/()
Linked list
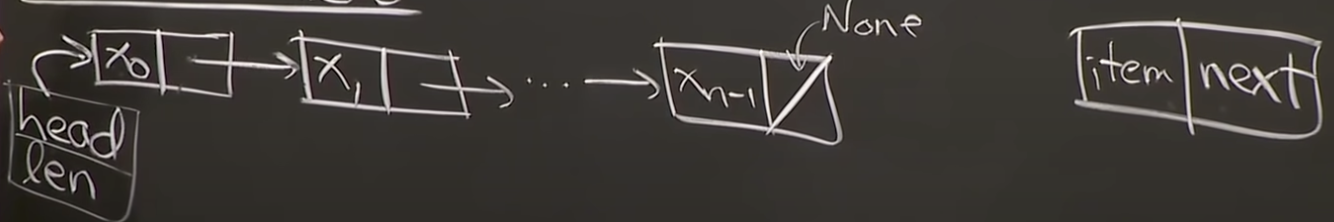
Dynamic seq.ops
static array
- inset / delete = at() cost Θ(n) time
- shifting
- Allocate /copying
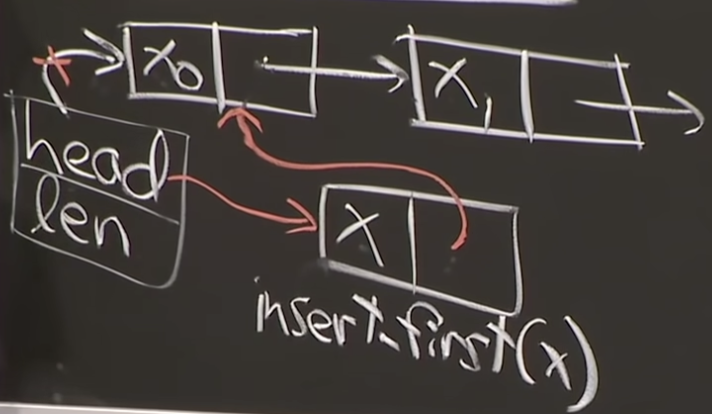
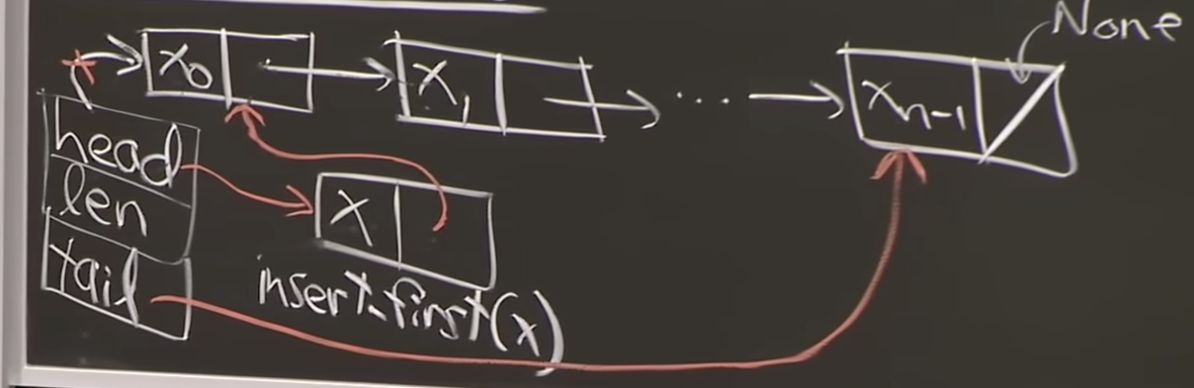
linked list
- insert / delete = first() O(1) time
- Insert/delete first
- Get / set_at need Θ(i) time(Θ(n) worst case)
Dynamic arrays (Python lists)
relax constraint size(array) = n <- items in sequence
enforce size = Θ(n) & >= n
maintain A[i] = Xi
Inset_last(x). :add to end unless n == size
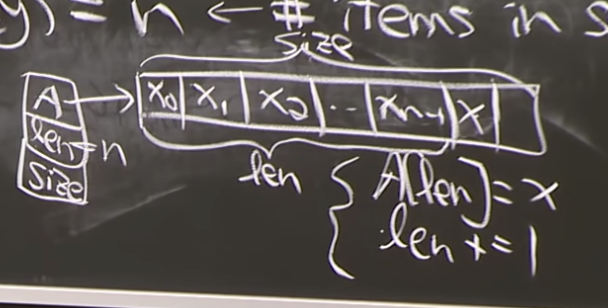
if n = size: allocate new array of 2*size
n insert_last() from empty array
resize at n = 1, 2, 4, 8, 16 ...
=> reize coset = Θ(1+2+4+8+16+ ...)
= Θ(long Z i=0 2^i) = Θ(2^log n) = Θ(n)
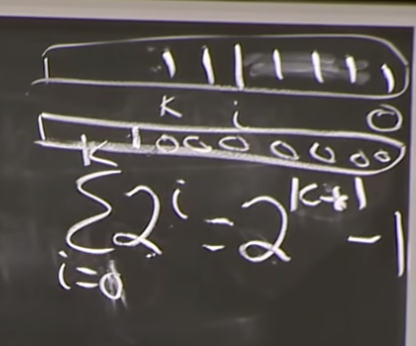
Amortization
operation takes T(n) amortized time
if any k operations take <= k*T(n) time
(averating over operation sequences)
Conclution

'CS' 카테고리의 다른 글
| [CS]Daemon이란? (2) | 2022.02.08 |
|---|---|
| [Algorithm] what is BigO? (0) | 2022.02.03 |
| [leetCode]LeetCode를 Github에 자동커밋하기 (3) | 2022.01.17 |
| [프로그래머스](level 2)피보나치의 수 (0) | 2022.01.10 |
| SAGA 패턴이란? (2) | 2022.01.06 |